|

|
From past experiences with kids and bubbles, Grandma thought of a different way for the Grandkids to burn off excess energy. |
|
Evidently Piper and Rachel love Grandma reading to them. She read the same *book over, and over, and over. They kept saying, "Gain Grandma, Gain." They both were VERY observant to EVERYTHING on the pages. They didn't miss not one thing from the previous time the story was read to them. It always amazes me the tolerance that kids have for repetition. It also reminded me how eager and sharp their young minds are. *Note: Grandma only brought one book with her. She won't make that mistake again. (Grandpa, no moaning and groaning.) |

|

|
Kilie was ever on the hunt for Symantha's cats, but she didn't win the tile of "Cat Chaser". That honor went to little Rachel. |
| Grandma with Armin on his special day. He grew so much just since the reunion! |

|

|
Abbie looks so very cute with her little curled bangs. She almost looks like she's already pleading for her Momma's forgiveness for an event that's bound to happen sometime in the near future! |
| Let's see how strong Symantha's futon is. |

|
 Brie loved that little baby glow worm. |

|
Grandma didn't have her glasses on when Abbie suckered her into taking a picture of the cute little frog that She "found" on Symantha's porch railing. |
| Cats are very possessive. This one has claimed the sink in the front bathroom. If I could rig up some way to remotely turn the water on, I'll bet I could cure her of sucking eggs... |

|

|
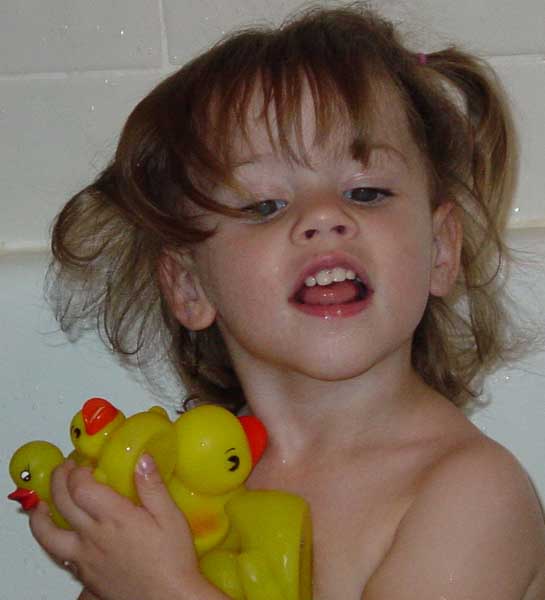
I caught Rachel peeking around the corner of the mirror while in the tub. |
| I can't wait for her to start dating....what a teasing she's going to get from her Brothers!!!! |
|

|
In a casual conversation at church, Brian Cox mentioned that he had always wanted to bicycle down Salt River Canyon. This sounded to me like opportunity was knocking so, after some discussion, we arranged a trip. |
| On July 10, at Oh-dark-thirty (actually, when I arose at 0300 hours it was argue-able light) we began the trip. Like most down hill jaunts, this was fun. It was also a bit scary. Early in the morning there was almost no traffic, and with my review mirror I can see what is approaching. Further, as my speed increases, I drift away from the side of the road and into the middle of the lane. Brian, on the other hand, didn't have a mirror and, fearing death by car, rode strictly on the six inches of pavement between the white line and the drop off into the dirt. |

|

|
We reached speeds in the high 30's and, on a couple of occasions when he encountered gravel, I thought Brian was headed for the hospital (or possibly the morgue). I had to look away, so I didn't actually see the miracle, but somehow he managed to stay upright, and we finish without incident. This gave my mantra from Scouts (any trip without fatalities was good one) a whole new meaning. |

On the road from Salt River Canyon back to Globe there is a section labeled as being a 6% grade, 8 miles long, and we had thought to ride that also. But mechanical problems continue to be my companion. Brian experienced a flat, and with his fancy European style tubes, I couldn't apply my slime base universal fix. So... that stretch of road continues to be another ride for another day. |
| On my way to Casa Grande last week, I hit a bird. I doubt that two data points establish a trend, but in the recent past it appears that big vehicles tend to hit big animals, and small vehicles tend to hit small ones. The impact was centered on the defect marking the weakest part of my windshield, and it may have produced some small cracks. What it did do was to cleanly remove the inside rear view mirror, which landed in my lap. Until it was gone, I didn't realize how often I acquire data from there. I must have glanced at that empty hole once every 15 seconds for the next 150 miles. |

|

|
The tree behind the rabbit house died last year, and Barbara asked David Ellis to come over and take it down. He brought an electric chain saw, and a half hour later, the job was done. We now have an unobstructed view of Jerry's new house, and my to-do list has another entry (haul the wood over to Ellis before next winter). |
| After dreading it for the better part of a year, we finally defrosted the freezer in the kitchen. Every time I start a project like that, I promise myself that, "this time I'm going to let the whole thing melt, and not chip the ice out a piece at a time." Right... By the time it was over, I had a mild case of frost bite, and the quick had been pulled away from the nail on several of my fingers (I didn't learn that until they warmed up the next day). |

|

|
We brought in all the ice chests to hold the frozen goods, and stacked them on the kitchen floor. Then we piled on additional insulation in the form of blankets. That worked so well that when it came time to re-stock the freezer, the ice cream was not even soft. |
| I didn't do any actual measurements, but I would guess that we increased the usable room in the freezer by somewhere between 50 and 100%. But just for the record, a chest type freezer holds much more than an upright. |

|

|
The shed out back of the house was old when we purchased this place in 1982, and the passage of time hasn't made it any more waterproof, so I have undertaken to install a new roof. The fastest, easiest, and cheapest way would have been to purchase a few 2 X 4s and nail everything back in place. |
| But, for some time now, I've wanted to build steel trusses, and I chose to let this project be the vehicle for fulfilling that desire. This has turned out to be much more labor intensive than I anticipated (when you get old, everything is more labor intensive than you anticipate). There are 550 short (4 to 6 inch) pieces of 5/8 inch rebar to cut, and then weld (top and bottom and front and back). With about 35% of the fabrication complete, I have used just over 15 lbs. of 1/4 inch welding rod. I didn't see that coming... |

|

|
I purchased a metal cut-off saw, and gave $10 for a one year (supposably no questions asked) warranty. I have been trying to get my money's worth out of it, and to this point it has functioned well (except that it is about ready for a new blade). The pieces that I have cut have exactly the right angle, and are easily within a millimeter of being the same length. Do that with a hack-saw! |
| Rebar has a ridge running along each side. Positioning that ridge as shown in this photo, moves the pieces apart slightly, and allows a larger surface for welding the butt joints. The trick is to get the weld made before this slot fills up with slag. |

|

|
I have always enjoyed welding (super glue for steel), but have never claimed to be particularly good at it. Since the integrity of the roof depends on these welds being permanent, I have worried some about my technique. It's always exciting when you don't know for sure that your crazy, hare-brained, ideas are actually going to work... |
| Who is this old geezer, and what has he done with my face? |

|

|
The last section of this communication is devoid of photos. It is also requires some thought, so the faint of heart may choose to stop reading at this point. It is, however, of interest to me so I choose to discuss it. The mathematical concepts employed herein are all covered in high school algebra.
|

|
As long as I can remember, I have liked music. It has been said, that someone who likes sausage or respects the law should never inquire too closely into how either of them are made. I may be tempting fate, but for some number of years now, I have been ruminating on the question of why, on a molecular level, is harmony pleasant and dissonance annoying. Recently, I happened on a website that delved into the physics of music and, after a little mathematical manipulation, experienced an epiphany. Nathen, if you look closely at this, you may decide that music is not as arbitrary as it at first seems...
Sound is vibrations propagated through some media (usually air, but water works also). The frequency of the vibrations (measured in cycles/second, or Hertz, abbreviated Hz), determines the pitch, with higher frequencies resulting in higher pitches. The first step in developing a musical scale is to define the frequency of some note, Fo. The most common convention is that a note called A is assigned a frequency of 440 Hz. The frequencies of all the other notes are then calculated by the formula: Fn = Fo (a)n where n is the number of intervals (called half-steps [why this name, I don't know]) that separate Fn and Fo. Positive values of n ascend the scale, and negative values descend it. In this equation, a is a constant equal to the twelfth root of 2, (approximate value = 1.059463094359). Replacing a with 2(1/12) gives: Fn = Fo (2(1/12))n From this equation it is evident that:
A, A#/Bb, B, C, C#/Db, D, D#/Eb, E, F, F#/Gb, G, G#/Ab, A. The rational behind this distribution of sharps & flats (# & b) is not intuitive. The ratio between of the frequency of the first note in a scale (Fn) and the frequency of any other note in that scale (Fn+c, where c is an integer between 0 and 12), is given by the equation (Fn+c)/(Fn) = (2(1/12))c
At this point my theory breaks down. Consider a minor chord. The bottom note is still called the "tonic." "Normalizing" gives the following ratios: This chord is harmonic, and most people think of it as sounding "sad." As far as I can ascertain, there is no simple fraction equal to the decimal 1.18921, so I am at a loss to explain why a note 3 half-steps up from the tonic sounds good as a chord member. Once I am able to solve that conundrum, all I will have left, is to figure out how cadence, rhythm, and rhyme interact with harmony. (Ok, so I'm still pretty close to the starting point, but at least I have a starting point...)
Fn = Fo (a)n. When a is equal to 2(1/4) the "octave" will be composed of 4 half-steps; when a is equal to 2(1/8) the "octave" will be composed of 8 half-steps; when a is equal to 2(1/16) the "octave" will be composed of 16 half-steps; etc. For several values of a I have tabulated the ratios of the frequency of each half-step in the scale to the frequency of the starting note using the formula:
|
| There are a lot of number here, and without actually hearing these ratios it is impossible to know how they will sound. It is interesting to note that very few of them have ratios of frequencies approximating both 1½ and 1¼, the combinations that are "harmonic" in the commonly used 12 half-step scale. My guess is that none of these other scales will produce combinations that are pleasurable to the ear, and that is why we use what we use. Still, creating and experiencing these music systems based on different intervals would be an interesting experiment. Maybe some day when I get some time... |